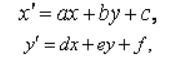Ну … да … в идеале надо но искажения не настолько влияют на результат. Как никак качество оптики сейчас не самое плохое.
Линзы без аберраций изобрели в 2019 году, два года назад? У Вас супер передовые линзы?
Это так же называется геометрические искажения Линз.
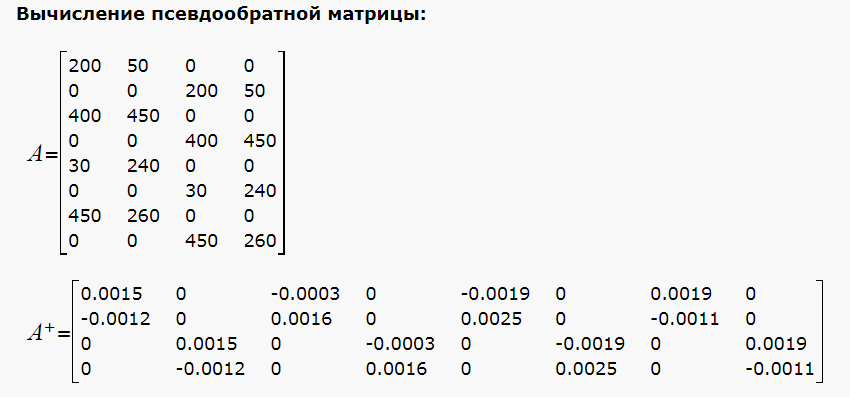
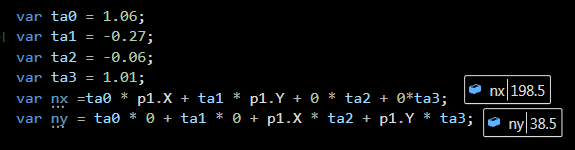
Делал Я поиск решения положения камеры её фокуса. По координатным методом за 1 час находит все параметры камеры, включая перспективу, наклон и у первый коэффициент нелинейных искажений линзы.
На графике показан срез функционала, там куча локальных минимумомв.
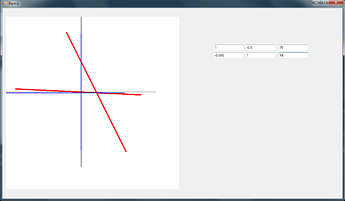
Задача калибровки выяснить параметры камеры. У нас есть шахматная доска и есть камера.
Она снимает шахматную и на экране мы видим рисунок с некоторыми искажениями. на GIF центральные точки квадратов помечены кружком.
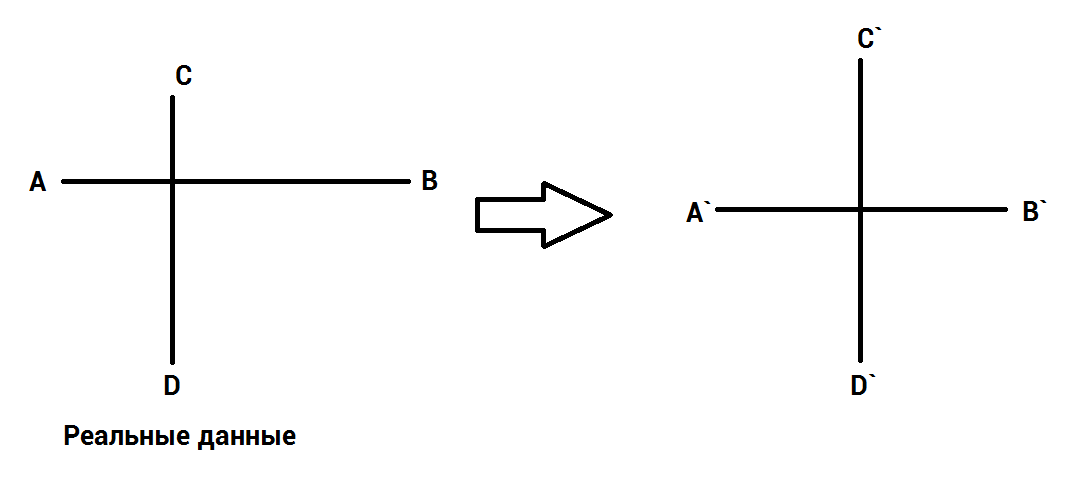
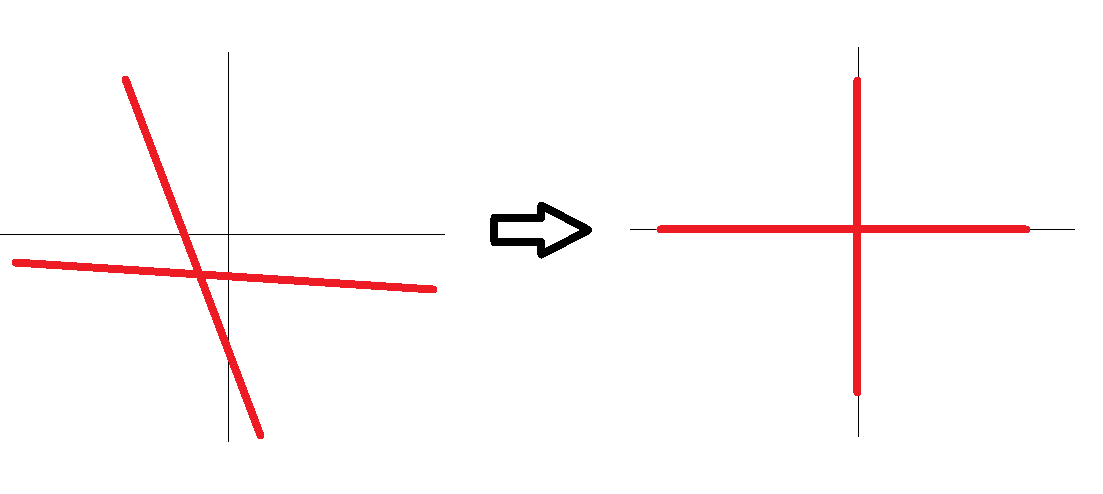
1)Параллельные прямые собираются в точку, а иногда и в три точки. Горизонтальные вертикальные и перпендикулярные каждые линии собираются в свою точку.
2)Квадраты становятся пухлыми округлыми. А плоская доска похожа на подушку или бочку.
3)А если присмотреться, то прямые линии становятся кривыми.
4)А если в кадр попадает девушка, то у ней моментально прибавляются килограммы.
5)Даже неподвижные объекты выглядывают друг из-за друга стараясь попасть в кадр.
6)Ах да и основное чуть не забыли центр доски не по центру кадра.
Задача калибровки устранить все эти искажения. Для чего нам надо разработать модель камеры.
Внешние параметры камеры. Это положение камеры в пространстве мира-сцены.
Положение камеры 3 параметра Cam.T=(x,y,z) и 3 угла Эйлера Cam.YPR=(Yaw,Pitch,Roll)
Еще не стоит забывать что у доски тоже самое.
Положение доски 3 параметра Board.T=(x,y,z) и 3 угла Эйлера Board.YPR=(Yaw,Pitch,Roll)
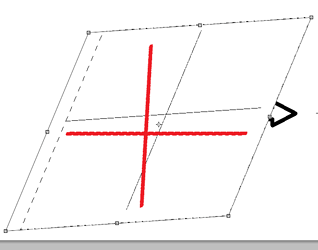
Они кодируют смещение точек на фото. А так же вращение относительно точки на экране.
Оставшиеся углы кодируют сжатие и растяжение по горизонтали и вертикали.
Внутренние параметры.
У камеры есть фокусное расстояние cam.D. Оно связано с углом обзора. И при этом создаёт перспективу.
Есть матрица камеры но она может быть установлена неровно относительно линзы.
Из за чего нарушается соотношение сторон пикселей. cam.Aspect (Выше было cam.a)
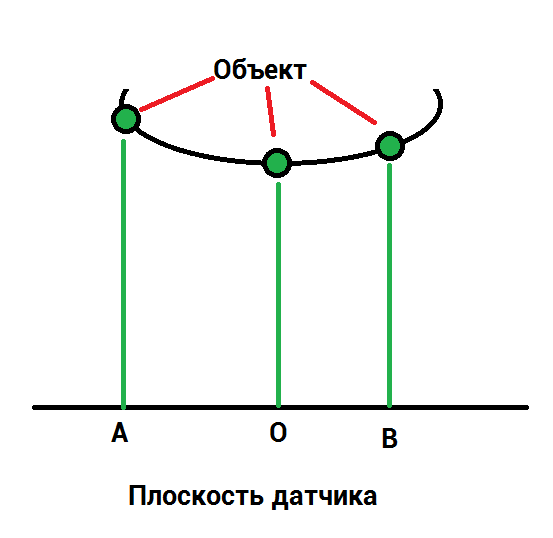
В потогонных трубах стоит пара линз которая должна скомпенсировать перспективное искажение.
Однако оптическая система линз не идеальна и создаёт геометрическое искажение по краям картинки более узкая, а по серёдке более. Будем называть это дисторсией линз.
Даже система из единичной линзой не идеальна и с фронтальной и тыльной стороны имеют разный радиус кривизны. Будем использовать приближение первого порядка.
Тут k- это коэффициент определяющий геометрические искажения линзы.
// Оператор геометрических искажений от линзы.
function L(x,k,r:Real):Real; Overload;
begin
if ((1+k*r*r)=0) then result:=MaxInt else result:=x/(1+k*r*r);
end;
function L(v:TPoint2DReal; k3:Real):TPoint2DReal; Overload;
var r:Real;
begin
r:=Hypot(v.x,v.y); // расстояние от 0 до точки, Hypot точнее чем sqrt. Result.x:=L(v.x,k3,r);
Result.y:=L(v.y,k3,r);
end;